Aiuto allo studio in STATISTICA per medie e superiori: mix di esercizi miei e di attinti da varie fonti
Scusa la banalità di questa bozza di appunti.
Potresti trovare utili links in web, ad es.: studenti, youmath, ...
Potresti digitare in Google differenza tra media, mediana, moda
[Pagina senza pretese di esaustività o imparzialità, modificata 04/10/2024; col colore grigio distinguo i miei commenti rispetto al testo attinto da altri]
Pagine correlate: matematica x medie e sup; calcolo combinatorio, calcolo delle probabilità
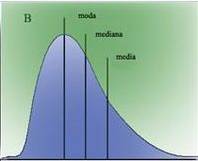
Distribuzione statistica di dati
(in ordinata le frequenze di ricorrenza dei dati indicati in ascissa)
La MEDIA è il rapporto tra la somma dei dati numerici messi in ascissa e il numero dei dati
La MODA è il valore che si presenta con maggiore frequenza
La MEDIANA è il valore centrale tra i dati numerici espressi in ascissa in ordine crescente
↑2024.06.01 <foglio > Informazione, scienza e metodo scientifico fra Karl Popper e Claude Shannon. vi è una ragione specifica per la quale il metodo scientifico è il migliore quando si tratti di acquisire conoscenza, e non solo informazione. Lungi dall’essere un difetto, il tipo di certezza statistica - o per meglio dire il tipo di confinamento del grado di incertezza, mediante statistica e metodo sperimentale - è precisamente il vantaggio che consente alla scienza di evolvere e migliorare, invece di rimanere immota di fronte a fatti nuovi o alla scoperta di errori, come avviene per la pseudoscienza, il pensiero magico o la religione.
↑2019.05.02 i 23 alunni (A, B ... Z) di una classe indicano quanti minuti impiegano solitamente per raggiungere la scuola: A 20, B 12, C 3, D 7, E 5, F 6, G 15, H 5, I 10, L 4, M 7, N 5, O 6, P 9, Q 5, R 6, S 7, T 10, U 7, V 10, X 18, Y 2, Z 5
Per calcolare la MEDIA dei tempi basta fare la somma dei tempi e dividere per 23
MEDIA μ=184/23=8
Per calcolare la MEDIANA (detta anche mediana campionaria) dei tempi è necessario disporre in ordine crescente i 23 valori che indicano i tempi di percorrenza
Y 2
C 3
L 4
E 5
H 5
N 5
Q 5
Z 5
F 6
O 6
R 6
D 7
M 7
S 7
U 7
P 9
I 10
T 10
V 10
B 12
G 15
X 18
A 20
e quindi individuare il valore centrale che è alla 12ª posizione, il valore 7
Se la sequenza avesse avuto un numero pari di elementi, anziché dispari, avremmo considerato i due valori centrali e avremmo preso per MEDIANA la media tra loro due.
Per calcolare la MODA (detta anche moda campionaria) dei tempi è necessario costruire la distribuzione di frequenza dei tempi, ossia associare ad ogni valore del tempo la sua frequenza assoluta, come in tabella
val frequenza di ricorrenza
2 1
3 1
4 1
5 5
6 3
7 4
9 1
10 3
12 1
15 1
18 1
20 1
23
Si vede che il valore più frequente è il 5.
Per calcolare la VARIANZA (detta anche media ponderata degli scarti quadratici) è necessario affiancare alla suddetta tabella delle frequenze gli scarti di ogni valore rispetto alla media, farne i quadrati, e farne la media ponderata sulle frequenze
|
valore |
frequenza |
scarto |
scarto² |
scarto² |
|
2 |
1 |
-6 |
36 |
36 |
|
3 |
1 |
-5 |
25 |
25 |
|
4 |
1 |
-4 |
16 |
16 |
|
5 |
5 |
-3 |
9 |
45 |
|
6 |
3 |
-2 |
4 |
12 |
|
7 |
4 |
-1 |
1 |
4 |
|
9 |
1 |
1 |
1 |
1 |
|
10 |
3 |
2 |
4 |
12 |
|
12 |
1 |
4 |
16 |
16 |
|
15 |
1 |
7 |
49 |
49 |
|
18 |
1 |
10 |
100 |
100 |
|
20 |
1 |
12 |
144 |
144 |
|
23 |
460 |
VARIANZA = media ponderata degli scarti quadratici = 460/23=20,00
↑2019.05.02 in 2000 casse di cuscinetti se ne trovano di guasti, con la seguente casistica: in 340 casse i cuscinetti sono tutti buoni, in 360 casse si trova un cuscinetto guasto per ciascuna, in 500 casse se ne trovano 2 di guasti per ciascuna, in 400 casse 3 guasti/u, in 200 casse 4 guasti/u, il 160 casse 5 guasti/u, e in 40 casse 6 guasti ciascuna; calcolare MEDIA, MEDIANA, MODA, VARIANZA
Soluzione:
ci è stata indicata la casistica in ordine crescente di numero guasti trovati in ogni scatola (se ci avessero fornito i dati in ordine casuale, avremmo dovuto primariamente costruire la tabella in ordine crescente di valori, come segue)
|
x |
freq. |
freq. |
x |
x - media |
scarto² |
scarto² |
|
0 |
340 |
17,0% |
0 |
-2,2 |
4,84 |
1.645,60 |
|
1 |
360 |
18,0% |
360 |
-1,2 |
1,44 |
518,40 |
|
2 |
500 |
25,0% |
1.000 |
-0,2 |
0,04 |
20,00 |
|
3 |
400 |
20,0% |
1.200 |
0,8 |
0,64 |
256,00 |
|
4 |
200 |
10,0% |
800 |
1,8 |
3,24 |
648,00 |
|
5 |
160 |
8,0% |
800 |
2,8 |
7,84 |
1.254,40 |
|
6 |
40 |
2,0% |
240 |
3,8 |
14,44 |
577,60 |
|
2.000 |
100,0% |
4.400 |
4.920,00 |
Per calcolare la MEDIA dei guasti per scatola basta fare la media ponderata sulle frequenze, cioè MEDIA μ=(0·340+1·3601+...+6·40)/2000=4400/2000=2,2 cuscinetti guasti per scatola
La MODA è il valore più frequente: 2 cuscinetti guasti per cassa (ricorre con freq.500, la massima)
La MEDIANA è il valore centrale tra i dati numerici messi in ordine crescente: la lista è pari e dunque i valori centrali sono 2, a posizione 1000 e a posizione 1001: fino al posto 340 troviamo 0; da 341 a 700 troviamo 1; da 701 a 1200 troviamo 2; quindi la MEDIANA è 2
La VARIANZA = media ponderata degli scarti quadratici = 4920/2000 = 2,46
La DEVIAZIONE STANDRD = radice quadrata della varianza = 1,57
↑2013.12.19 <sussidiario> SCIENZA E METODO - un approccio generale al Metodo Scientifico: l'autore (Gianpaolo Bellini fisico) tratteggia sinteticamente le caratteristiche del potere conoscitivo delle Scienze della Natura con la loro caratteristica peculiare: essere sperimentali. Osservazione sperimentale > misurazione matematica > probabilità statistica > modello > riproducibilità > legge > teoria. Continua qui.