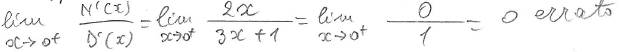LIMITI con la regola di De l'HOPITAL (o teorema di de l'Hôpital o di de l'Hôspital)
la regola è applicabile solo in un contesto che rispetti precisi vincoli: essa consente di calcolare, verso gli estremi di un intervallo (a,b), il limite di un rapporto di funzioni [lim f(x)/g(x)] considerando il limite del rapporto tra la derivata del numeratore e la derivata del denominatore [lim f(x)/g(x) = lim f'(x)/g'(x)] per x→a+; il ragionamento è analogo per x→b-; ma, ripeto, la regola è applicabile solo se sono rispettate precise ipotesi (condizioni, vincoli):
1) f(x) e g(x) devono essere funzioni derivabili nell'intervallo (a,b) considerato (essendo a, b valori finiti o ∞);
2) il lim f(x)/g(x) per x→ a+ deve essere una forma di indeterminazione del tipo 0/0 o ∞ /∞
3) la derivata g'(x) non deve essere mai nulla nell'intervallo considerato
4) deve esistere (finito o ∞) il lim f'(x)/g'(x)] per x→ a+
Le condizioni si possono ripetere per x→b-
La regola in titolo in realtà è da attribuirsi a Johann Bernoulli, suo insegnante
- <wikip> definizione della regola
- <youmath.it> Esempi di esercizi relativi
[Pagina senza pretese di esaustività o imparzialità, modificata 2023.11.27; col colore grigio distinguo i miei commenti rispetto al testo attinto da altri]
Pagine correlate: matematica medie e superiori; limiti notevoli, studi di funzione
↑2023.11.26 qui altri esercizi svolti (scusa la brutta calligrafia)
↑2019.05.15 il seguente limite in forma indeterminata si potrebbe risolvere anche senza De l'Hopital (come qui 2018.11.19), ma con De l'Hopital (visto che ci sono le condizioni per la sua applicabilità) in questo caso è più facile
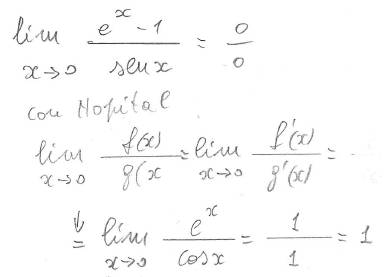
altro caso semplice
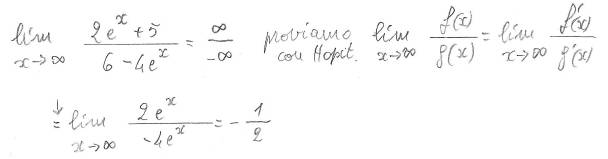
semplice anche quest'altro se ricordi come si fa la derivata di una funzione di funzione (f(g(x)))' = f'(g(x).g'(x)
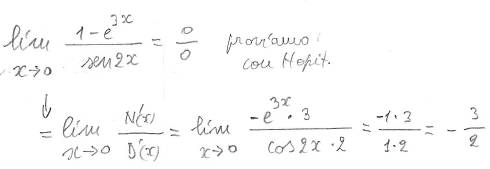
e, analogamente, quest'altro esercizio
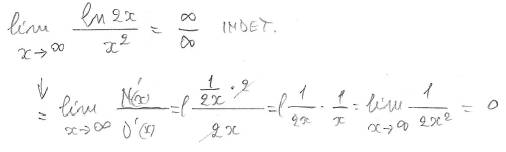
RICONDURRE A FORMA trattabile con regola di De l'Hopital
Può capitare che la funzione di cui cercare il limite non si presenti nella forma f(x)/g(x), ma che sia riconducibile a tale forma, per poi applicare Hopital
Esempio di forma f(x)∙g(x) trasformabile in forma N(x)/D(x)
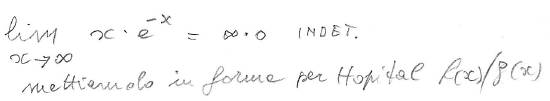
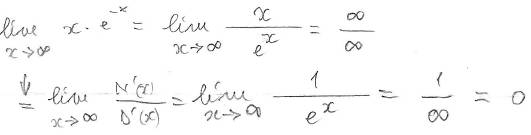
Occorre provare a cambiare forma se quella scelta non portasse a risultato: ad esempio, per l'esercizio qui sopra, se avessimo scritto,
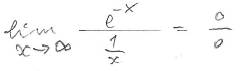
e avessimo provato con Hopital così
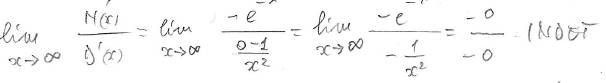
non avremmo risolto il problema.
Esempio di forma f(x) - g(x) trasformabile in forma N(x)/D(x)
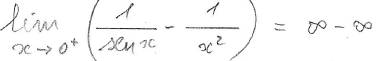
facciamo comun denominatore
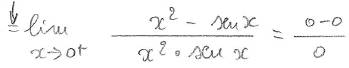
ed arriviamo a forma trattabile con Hopital
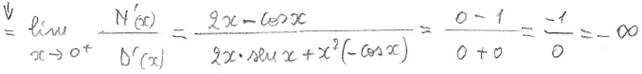
Anche il seguente caso sarebbe una forma (∞ - ∞) trasformabile in forma N(x)/D(x), ma attenzione a non usare impropriamente Hopital
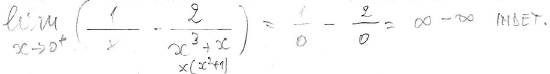
possiamo fare comun denominatore e risolvere senza Hopital
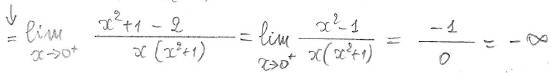
Hopital non è applicabile perché non è forma indeterminata 0/0 o ∞/∞. Se incautamente applicassimo Hopital, violando il suddetto vincolo, arriveremmo a conclusione sbagliata