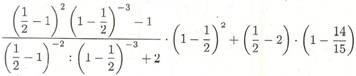Allenamento MATE 1ª superiore

[Pagina senza pretese di esaustività o imparzialità, modificata 15/05/2024; col colore grigio distinguo i miei commenti rispetto al testo attinto da altri]

 

↑2019.10.gg per prima superiore: un paio di esercizi  per ciascuno dei 5 argomenti

1) operazioni con le potenze

1a)

1b) [(-2/3)^-11(3/2)¹²(-2/3)³]:(-2/3)^-18

1c) [(-12)⁴ + (-144)³] / 12⁴  (prova 2019.09.30)

1d) {[-(-2,4∙10³)²] / 2,4}^-1

1e) [(-3/4)^-5(4/3)⁶(-3/4)⁹]:(-3/4)^-1

 

2) scomponi in fattori

2a) (2a - 1)³ + 2a²(a²/2 - 4a + 2) - (a + 2)²(a - 2)²

2b) x⁴ - 2x³ - x² + 4x - 2  2c) 8b⁵ -12b⁴ +6b³ - b²

2d) 27a³ - 8b³ (vedi differenza o somma di due cubi) ;

2e) 4x² - 6xy + 9y² falso quadrato: scomponi in un rapporto di binomi

2f) a² - 10a + 25 - b²  (vedi la diff di 2 quadrati?)

2g) 2x² + x – 6 (vedi “somma prodotto”)

2h) x³ - 7x + 6

2i) verifica che la seguente espressione è un quadrato perfetto
9/4x^2m + 4y²ⁿ + 9x^4m+2y⁴ + 6x^myⁿ - 9x^3m+1y² - 12x^2m+1yⁿ⁺²  

 

3) semplifica, previa precisazione delle condizioni di esistenza (C.E.); classifica le espressioni

   3a) (y³ - 9y² - y + 9) / (y² - 10y + 9); per quale valore di y l'espressione varrebbe 1/4

3b)		Per quale (quali?) valore di x l'espressione varrebbe 0?
3c)		Per quale (quali?) valore di x l'espressione varrebbe 0?

   3d) per quale valore di x la seguente espressione varrebbe 0?
      [x / (x - 1)] - [(x + 3) / (2 - 2x)] - [(x² + x + 1) / (x² - x)];

   3e) semplice da risolvere e classificare: (x-2)/4 – (x+2)/2 –x/4 +3/2

 

4) determina il valore dell'incognita

4a) pago a rate un importo x: 1/5 in prima rata; i 3/4 del restante in seconda rata; il saldo con 400€: quanto valeva x?

4b) la base di un triangolo isoscele misura 12 cm ed è i 3/8 del perimetro: calcolane l'area

4c) determina k in modo che il polinomio (x³ - 2x² + kx + 8) sia divisibile per x+2

4d) determina k in modo che il polinomio (x³ +kx² + 2x - 4) sia divisibile per x-2 

4e) dimostra che la differenza dei quadrati di due numeri naturali che differiscono di 2 è un multiplo di 44f) dimostra che la differenza dei quadrati di due numeri naturali che differiscono di 3 è dispari

5) geometria

5a) vedi criteri di congruenza di triangoli

5b) dimostra perché è impossibile che un triangolo nel piano abbia i lati che misurano 143u, 216u, 372u, essendo u qualunque unità di misura

5c) dimostra che in un parallelogramma le bisettrici degli angoli alla base si incontrano ad angolo retto.

5d) sui lati congruenti AC e BC di un triangolo isoscele ABC con vertice in C, fissa rispettivamente i punti P e Q tali che AP sia congruente con BQ; le rette AQ e BP si intersecano in M; dimostra che la retta CM è bisettrice dell'angolo in C e mediana di AB.

5e) un triangolo isoscele ABC con vertice in C ha gli angoli alla base di 36°; prolunga il lato BC (sulla retta BC dalla parte di C) di un segmento CD congruente ad AC; calcola l'ampiezza dell'angolo DAC.

 

↑2019.11.20 il cosiddetto metodo di “somma prodotto” per la scomposizione di un trinomio completo di secondo grado in una variabile, del tipo ax² + bx + c, consiste nel trovare due numeri m ed n tali che il loro prodotto faccia (a∙c) e la loro somma faccia b; in tal caso è possibile scomporre b in m+n e poi procedere col raccoglimento parziale; se a=1 si può passare direttamente alla scomposizione così x² + bx + c = (x + m) (x + n), con m ed n tali che m+n=b ed m∙n=c.

Ecco un esempio nel caso più generale con a≠1

2x² + x - 6

Cerchiamo due numeri che moltiplicati facciano 2∙(-6)=-12 e sommati facciano 1 (sono 4 e -3)

2x² + x - 6 = 2x² + 4x – 3x - 6 = 2x∙(x + 2) - 3(x + 2) = (x + 2) (2x - 3)

Nulla vieta che si provi a scomporre con Ruffini oppure che si scomponga con le due soluzioni (se esistono) dell’equazione di 2° grado ax² + bx + c = 0

ax² + bx + c = a∙(x - x₁) (x - x₂) dove x_1,2 = [-b ± Radq(b² - 4ac)]/2a;

nel nostro caso x_1,2 = [-1 ± Radq(1+48)]4 = (-1 ± 7)/4 → [x₁ = -2; x₂ = 3/2)]

2x² + x - 6 = 2∙(x + 2)∙(x - 3/2) = (x + 2) (2x - 3)