Esempi di esercizi su LEGGI DI NEWTON e DINAMICA (per scuola secondaria)
<wikipedia, youmath, library> Prima, seconda e terza legge di Newton
Consulto fra gli altri il testo <Fisica.James S.Walker>
Scusa ove ravvisassi banalità; ti sarei grato se mi segnalassi errori.
[Pagina senza pretese di esaustività o imparzialità, modificata 21/03/2022; col colore grigio distinguo i miei commenti rispetto al testo attinto da altri]
Pagine correlate: cinematica, Lavoro, energia cinetica e potenziale, quantità di moto, aiuto allo studio, matematica
↑2019.09.20 Forze e vettori, loro composizione con angolo anche ≠ 90°.
Una palla da volley avente massa 275g viene schiacciata con una forza di modulo 5,1N, avente direzione che fa un angolo di 20° con l'orizzontale. Calcola il modulo della forza totale che agisce sulla palla schiacciata.
L'angolo tra la forza peso e la forza di schiacciata è di 70° (vedi angoli complementari nel triangolo rettangolo formato dalle direzioni delle due forze con l'orizzontale).
Il modulo del vettore somma si calcola con la seguente formula (qui spiegata)
c = Radq(a² + b² + 2ab∙cosα) dove c è il modulo del vettore somma dei vettori di modulo a e b.
Vedi la suddetta formula qui implementata in Excel [6,5N].
Analogamente potresti calcolare la risultante delle due forze di 85N e 62N trainanti una slitta con angolo di 23° fra loro [144N].
↑2019.05.04 alcuni esercizi svolti su questa tabella excel su piano inclinato e forza d'attrito.
↑2019.02.20 nella savana un predatore e una preda di massa rispettivamente 55 kg e 30 kg si vedono da fermi e scattano nello stesso momento (la preda in fuga e il predatore in rincorsa) accelerando per 3 secondi (poi proseguirebbero nella corsa con la velocità limite che hanno raggiunto); sapendo che il predatore accelera con una forza di 495 N e la preda con una di 240 N, misura la velocità limite raggiunta dal predatore e quella raggiunta dalla preda.
Indichiamo con il pedice1 il predatore e con pedice2 la preda; quindi con v1 intendiamo la velocità limite del predatore e con v2 quella della preda; analogamente per le masse m1 e m2 e per le accelerazioni a1 e a2.
La loro velocità iniziale v0=0. Dalla seconda legge di Newton (F=m·a) ricaviamo:
a1=F1/m1=495/55=9m/s² v1=v0+a·t=0+9·3=27m/s
a2=F2/m2=240/30=8m/s² v2=v0+a·t=0+8·3=24m/s
Osserviamo che la velocità massima del predatore è superiore a quella della preda, che, dunque, presumibilmente sarà raggiunta.
↑2011.01.24 ATTRITO DINAMICO
Un'automobile di massa m = 1300 Kg viaggia a 65 Km/h. Improvvisamente l'autista vede un ostacolo e frena. Sapendo che il coefficiente di attrito (dinamico, kd) tra asfalto e pneumatici è di 0,75, calcola:
a) Quanto tempo impiega l'automobile a fermarsi
Trasformo la velocità da Km/h a m/s → v=18,06 m/s
La forza (resistente) di attrito dinamico è Fa = kd·Fp = kd·m·g
da cui a = Fa/m = kd*·m*·g/m = kd*·g (che intenderemo negativa se assumiamo velocità positiva)
sparisce la massa: il suo valore è ininfluente sul risultato che cerchiamo
vf = vi - a·t → 0 = vi - a·t
ricavo t = (0 - vi)/(-a) = vi/a = vi/(kd·g) = 18,1 / (0,75*·9,8) = 2,46s
b) Quanto percorre l'automobile da quando l'autista inizia a frenare (cioè lo spazio di frenata).
s = s0 + v0·t + 1/2·a·t² = 0 + v0·t + 1/2·kd·g·t² = 66,53 m
↑2011.01.22 traggo da <Fisica.James S.Walker> una massa (m1) di 20 grammi (20g=0,020kg) è attaccata a una corda lunga 120 cm (1,2m) e si muove lungo una circonferenza orizzontale con una velocità costante di modulo 1,50 m/s. Trascura gli attriti, trascura la massa della corda e considera la corda inestensibile. Quanto misura l'angolo α formato dalla corda con la perpendicolare passante per il centro della circonferenza?
Scomponiamo la forza peso Fp della m1 in due componenti col parallelogramma ABCD
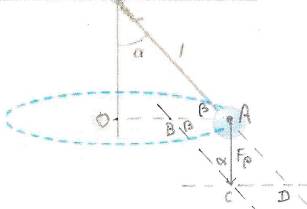
- la componente AD, in direzione della corda, è annullata dalla inestensibilità della corda;
- la componente AB in direzione radiale configura la forza centripeta, Fpc
- i due angoli siglati β sono congruenti perché alterni interni tra rette parallele, quindi l'angolo ACB è congruente con α
- r = 1,20∙sinα
- Fp∙= m1∙g (g accelerazione di gravità: 9,81m/s²)
- Fpc = Fp∙tanα
- tale forza centripeta è equilibrata dalla forza centrifuga che vale massa per accelerazione centrifuga (quest'ultima vale v²/r): Fc = m1∙v²/r
L'equazione che ci permetterà di trovare α sarà dunque Fpc = Fc in valore assoluto
m1∙g∙tanα = m1∙v²/r
semplifichiamo per m1 (sparisce la massa), il che significa che la massa è ininfluente sul risultato del quesito, ovvero è un dato ridondante, ovvero avrebbero potuto non darci il valore della massa rotante:
g∙tanα = v²/r
g∙tanα = v²/(1,20∙sinα)
tanα∙sinα = v²/1,20/g) = 0,191
sin²α /cosα = 0,191
(1 - cos² α) = 0,191∙cosα
-cos² α - 0,191∙cosα + 1 = 0
(cosα)1,2 = [0,191± Radq(0,191² + 4)]/-2
(cosα)1 = -1,1 da scartare perché impossibile
(cosα)2 = 0,909 dal che
α = arccos(0,909) = 24,6°
↑2011.01.20 traggo da <Fisica.James S.Walker> su un piano inclinato di 30° rispetto all'orizzontale è collocato un blocco A di massa 3kg, trattenuto verso l'alto da una corda che, scorrendo su una carrucola posta al vertice superiore del piano inclinato, è tesa verso il basso da un blocco B di massa 2,5kg. Trascuriamo gli attriti e lasciamo il sistema dei due blocchi libero di muoversi: il blocco B si muoverà verso l'alto o verso il basso? Con che accelerazione?
La componente obliqua F1 della forza peso del blocco A
FA = 3∙9,81∙sin30 = 1,5∙9,81 (sin30 = 0,5)
agisce nel verso opposto alla forza peso del blocco B
FB = 2,5∙9,81
dal che si vede che prevale FB e dunque il blocco B si muoverà verso il basso.
A prescindere dagli attriti il sistema dei due blocchi si muoverà con accelerazione data dalla risultante delle forze diviso la massa del sistema che si muove
a = (FB - FA ) / (mA + mB) = (2,5 - 1,5)∙9,81 / 5,5 = 1,78m/s² verso il basso
↑2010.08.27 traggo da <Fisica.James S.Walker> una massa di 40g viene attaccata ad una molla verticale di costante elastica k=20N/m e fatta abbassare lentamente (senza farla oscillare) finché la molla non si allunga più: calcola di quanto si allunga la molla.
Detto a l'allungamento,
F=0,04Kg∙9,8m/s²
k=20N/m
F=k∙a, dunque a=F/k
a=0,04*9,8/20=0,0196m
↑2005.mm.gg <unimi> esempi di esercizi risolti per Biologia UniMI