Esempi di esercizi di fisica – CINEMATICA, per scuola secondaria

- <goog ym> moto rettilineo: <ym> formulario, <ym> velocità media (vm=Δs/Δt) ed istantanea (idem con Δt→0) e <ym> legge oraria (s = s₀ + vm*t), dove s=spazio percorso, s₀=spazio iniziale.

- <ym> moto uniformemente accelerato: accelerazione (a=Δv/Δt) costante;
s = s₀ + v_0∙t + ½∙a∙t² detta legge oraria
v² = v₀²+2a∙Δx dal che vedi come lo spazio di frenata dipende dal quadrato della velocità iniziale.

- moto parabolico

- moto circolare, moto armonico

- Leggi di Newton.

Scusa ove ravvisassi banalità.

[Pagina senza pretese di esaustività o imparzialità, modificata 05/10/2024; col colore grigio distinguo i miei commenti rispetto al testo attinto da altri]

Pagine correlate: Dinamica, apprendimento, conoscenza, aiuto allo studio, matematica x MedEsup

↑2010.11.18  Da un dirupo alto 32,5m lasci cadere una palla (P₁). In seguito lanci una seconda palla (P₂) verso il basso con una velocità iniziale di 11,0 m/s.

d1) Quale palla ha il maggiore incremento di velocità quando raggiunge la base del dirupo?

d2) GIUSTIFICA la risposta con il calcolo.

PRIMA CONSIDERAZIONE

Detto Δv₁ l’incremento di velocità della P₁, detto Δv₂ quello della P₂, di primo acchito verrebbe da rispondere che Δv₁=Δv₂, perché entrambe le velocità (v₁ e v₂) aumentano per effetto della medesima accelerazione di gravità (a=9,81 m/s²); ma vediamo in dettaglio.

d1.1) CALCOLIAMO L’INCREMENTO DI VELOCITÀ Δv₁ della P₁

Scelgo sistema di riferimento tale che “spazio iniziale s_i = 0”, cioè partiamo dal ciglio del dirupo; scelgo positiva la direzione verso il basso, quindi segneremo la accelerazione di gravità come positiva.

Intendendo t = t₁, v_i la velocità iniziale della P₁, s_f lo spazio finale (percorso dal dirupo alla base), ricaveremo t dalla legge oraria

s_f = s_i + v_i t + ½ a t²

32,5 = 0 + 0 t + ½ 9,81 t², dal che ricavo

t² = 32,5 / (½ 9,81) da cui t=±RadQ(...)=2,574 secondi (trascuriamo il valore negativo del tempo)

Ora che conosciamo il tempo t impiegato dalla P₁ per arrivare alla base, calcoliamo con che velocità v_f arriverà alla base, considerando che parte da ferma (v_i =0)

v_f = v_i + a t

v_f = 0 + 9,81 2,574 = 25,252 m/s (vedi anche metodo di soluzione alternativo)

Δv₁ = v_f - v_i = 25,252 m/s

d1.2) CALCOLIAMO L’INCREMENTO DI VELOCITÀ Δv₂ della P₂

Intendendo t = t₂, v_i la velocità iniziale della P₂, s_f lo spazio finale (percorso dal dirupo alla base), ricaveremo t dalla legge oraria

s_f = s_i + v_i t + ½ a t²

32,5 = 0 + 11 t + ½ 9,81 t², ossia un’equazione di 2° grado in t

½ 9,81 t² + 11 t – 32,5 = 0, che risolviamo con la nota formula del t_1,2= [–b ± RadQ(b² - 4ac)]/2a

t_1,2= [–11 ± RadQ(11² + 2 9,81 32,5)] / 9,81 = 1,686 secondi, trascurando il valore negativo

Ora che conosciamo il tempo t impiegato dalla P₂ per arrivare alla base, calcoliamo con che velocità v_f arriverà alla base, considerando che non parte da ferma (v_i = 11m/s)

v_f = v_i + a t

v_f = 11 + 9,81 1,686 = 27,544 m/s (vedi anche metodo di soluzione alternativo)

Δv₂ = v_f - v_i = 27,544 – 11 = 16,544 m/s

Quindi Δv₁>Δv₂.

d2) Come GIUSTIFICARE la risposta?

Anche se l'accelerazione è uguale in entrambi i casi, essa agisce sulla P₂ per meno tempo rispetto a quanto agisce sulla P₁ perché la P₂, avendo velocità iniziale maggiore di quella della P₁, impiega meno tempo della prima per arrivare alla base; dunque, se l'accelerazione di gravità agisce per più tempo sulla P₁ che sulla P₂, procurerà alla P₁ un incremento di velocità maggiore che alla P₂ ( Δv₁>Δv₂).

GIUSTIFICHIAMO con il calcolo:

considerando che Δv = v_f - v_i e che v_f = v_i + a t

otteniamo che Δv= v_i + a*t - v_i, quindi

Δv= a t cioè Δv è indipendente dalla v_i: è dipendente solo dalla durata t di azione dell’accelerazione a.

Se facciamo il rapporto tra i due incrementi di velocità, otteniamo:

Δv₁/ Δv₂ = a t₁ / a t₂ e, semplificando per a, otteniamo

Δv₁/ Δv₂ = t₁/t₂ : gli incrementi di velocità sono direttamente proporzionali ai tempi di percorrenza.

METODO di SOLUZIONE ALTERNATIVO (con la conservazione dell’energia)

Siccome il moto che stiamo trattando è la caduta di un grave, potremmo ricavare la velocità di fine caduta attraverso la legge di conservazione dell’energia (potenziale + cinetica) che all’arrivo deve avere un valore uguale a quello di partenza.

Per la P₁ abbiamo un’energia di partenza che è tutta e solo potenziale (m g h) mentre all’arrivo è tutta e solo cinetica (½ m v_f²) dove m=massa, g=9,81m/s², h=altezza di caduta, v_f=velocità raggiunta alla base:

m g h = ½ m v_f², dal che, semplificando per m, otteniamo

g h = ½ v_f², dal che

v_f² = ±RadQ(2 g h)

v_f = RadQ( 2*9,81*32,5) = 25,252 m/s, trascurando il valore negativo.

Per la P₂ abbiamo un’energia di partenza che è in parte cinetica (½ m v_i²) e in parte potenziale (m g h), mentre all’arrivo è tutta e solo cinetica (½mv_f²):

½ m v_i² + m g h = ½ m v_f², dal che, semplificando per m, otteniamo

½v_i² + g h = ½ v_f², dal che

v_f² = ±RadQ(v_i² + 2 g h)

v_f = ±RadQ(11² + 2*9,81*32,5) = 27,544 m/s, trascurando il valore negativo]

↑2016.10.05 Una palla cade da un’altezza di 15 m, arriva al suolo e rimbalza con una velocità di 10m/s.

d1) Qual è il modulo della velocità con cui la palla arriva a terra?

d2) a quale altezza massima arriva la palla dopo il rimbalzo?

d3) a quale altezza da terra si trova la palla mezzo secondo dopo il rimbalzo?

Il moto della palla è quello della caduta di un grave, quindi uniformemente accelerato con l’accelerazione di gravità a = 9,81 m/s²;  intendendo positiva la direzione verso il basso, la sua legge oraria sarà s = s_i + v_i t + ½ a t²

d1) per calcolare la velocità di arrivo, calcoliamo prima il tempo impiegato a cadere

dalla formula 15m = 0 + 0 + ½*9,81m/s²*t² possiamo ricavare il t impiegato per arrivare al suolo

t=±RadQ[15m/(½ 9,81m/s²)]=1,748s

Sappiamo che in un moto uniformemente accelerato

v_f = v_i + a t dove v_f è la velocità di arrivo al suolo

v_f = 0 + 9,81m/s²*1,748s = 17,155m/s

d1a) soluzione alternativa con la legge di conservazione dell’energia, tipicamente applicabile nel moto che stiamo trattando (la caduta di un grave): per tale legge l’energia (potenziale + cinetica) di partenza deve essere uguale a quella di arrivo. La palla parte da ferma, quindi la sua energia alla partenza è tutta e solo potenziale (m g h) mentre all’arrivo la sua energia è tutta e solo cinetica (½ m v_f²), dove m è la massa della particella, g l’accelerazione di gravità, h l’altezza del punto di partenza rispetto a quello di arrivo, v_f è la velocità raggiunta alla base:

m g h = ½ m v_f², dal che, semplificando per m, otteniamo

g h = ½ v_f², dal che

v_f² = ±RadQ(2 g h)

v_f = RadQ( 2*9,81*15) = 17,155 m/s, trascurando il valore negativo]

Notiamo che il modulo della velocità di arrivo al suolo è superiore a quello della velocità di rimbalzo, il che è logico, perché parte dell’energia cinetica si è trasformata in calore per effetto dell’attrito durante il rimbalzo.

d2) mantenendo come positiva la direzione verso il basso, osserviamo il moto come uniformemente decelerato con a = 9,81 m/s² rispetto alla velocità iniziale v_i = -10m/s. Per calcolare a che altezza arriva, calcoliamo prima quanto tempo impiega ad azzerarsi la velocità:

v_f = 0 = v_i + a t = -10m/s + 9,81 m/s²*t dal che ricaviamo t

t = 10m/s/9,81 m/s² = 1,019s

Per calcolare lo spazio percorso nel moto uniformemente decelerato, usiamo la solita legge oraria

s_f = |s_i + v_i t + ½ a t²| (prendiamo il valore assoluto |...|, perché altrimenti ci uscirebbe una misura negativa di spazio, avendo scelto come verso positivo quello di discesa anziché di risalita)

s_f = |0 - 10m/s*1,019s + ½*9,81*(1,019s)²| =|-5,096m| = 5,096m

d2a) soluzione alternativa con la legge di conservazione dell’energia, in base alla quale l’energia (potenziale + cinetica) di partenza deve essere uguale a quella di arrivo. La palla parte da quota zero con |v_i| = 10m/s (dove ha solo energia cinetica) ed arriva a fermarsi all’altezza h (dove ha solo energia potenziale), quindi imponiamo che

½ m v_i² = m g h, da dove, semplificando per m, otteniamo

½ v_i² = g h, dal che ricaviamo h

 h = ½ v_i² = ½*(10ms)²/9,81 = 5,096m

d3) basta applicare la legge oraria del moto uniformemente decelerato

s_f = |s_i + v_i t + ½ a t²|

s_f = |0 -10m/s*0,5s + ½*9,81m/s²*(0,5)²| = |-3,773m| = 3,773m

Ovviamente avremmo potuto risolvere sia d2) sia d3) prendendo come positiva la direzione di risalita: in tal caso avremmo considerato come positiva la velocità iniziale e negativa l’accelerazione di gravità:

v_i = 10m/s

a = -9,8m/s²

avremmo risolto d2) senza i valori assoluti (|   |) così

v_f = 0 = v_i + a t = 10m/s - 9,81 m/s²*t

dal che ricavi t = -10m/s/-9,81 m/s² = 1,019s

   s_f = s_i + v_i t + ½ a t²

   s_f = 0 + 10m/s*1,019s - ½*9,81*(1,019s)² = 5,096m

avremmo risolto d3) senza i valori assoluti (|   |) così

s_f = s_i + v_i t + ½ a t²

   s_f = 0 +10m/s*0,5s - ½*9,81m/s²*(0,5)² = 3,773m

↑2015.11.15 Descrivi il moto vario di un corpo la cui velocità è rappresentata dal grafico seguente e misura lo spazio percorso tra 0s e 50s

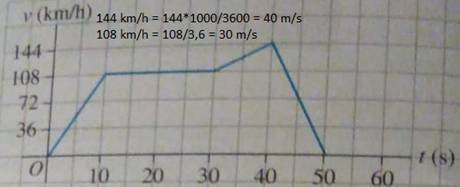
Premessa: trasformiamo i km/h in m/s per uniformare le unità di misura:

108km/h = 30m/s;     144km/h = 40m/s

Tra 0 e 10s vediamo che la velocità aumenta in modo costante per tutto il tempo Δt = 10s – 0s = 10s, quindi con accelerazione costante data da

a = Δv/Δt = (v_{f  -} v_i )/Δt ₌ (30m/s – 0m/s)/10s = 3 m/s²

trattasi di moto uniformemente accelerato che percorre uno spazio la cui legge oraria è data dalla formula

s_0-10 = s_i + v_i t + ½ a t² dove (s_0-10 = spazio percorso da calcolare nell’intervallo 0-10s, v_i = velocità iniziale = 0m/s, t = Δt intervallo di tempo = 10s)

s_0-10 = 0 + 0*10s + ½*3m/s²*(10s)²= 150m

Tra 10 e 30s vediamo che la velocità è costante per tutto il tempo Δt=30s-10s=20s: trattasi di moto rettilineo uniforme la cui legge oraria è data dalla formula

s_10-30 = s_i + v_i t = 0 + 30m/s*20s = 600m

Tra 30 e 40s vediamo che la velocità aumenta in modo costante per tutto il tempo Δt = 40s – 30s = 10s, quindi con accelerazione costante data da

a = Δv/Δt = (40m/s – 30m/s)/10s = 1 m/s²

trattasi di moto uniformemente accelerato che percorre uno spazio la cui legge oraria è data dalla già detta formula s_30-40 = s_i + v_i t + ½ a t²

s_30-40 = 0 + 30m/s*10s + ½*1m/s²*(10s)² = 350m

Tra 40 e 50s vediamo che la velocità diminuisce in modo costante per tutto il tempo Δt = 50s – 40s = 10s, quindi con decelerazione costante data da

a = Δv/Δt = (v_{f  -} v_i )/Δt = (0m/s - 40)/10 = -4 m/s²

trattasi di moto uniformemente decelerato che percorre uno spazio la cui legge oraria è data dalla suddetta formula s_40-50 = s_i + v_i t + ½ a t²

s_40-50 = 0 + 40*10 - ½*4m/s²*(10s)² = 200m

Concludendo: s_0-50  = 150 + 600 + 350 + 200 = 1300 m = 1,3 km

Nota che il valore numerico della misura dello spazio complessivamente percorso è uguale a quello dell’area sottesa alla linea spezzata che ne descrive la velocità, area formata dal triangolo rettangolo 0-10 più il rettangolo 10-30, più il trapezio 30-40 più il triangolo rettangolo 50-50

↑2010.11.10 Una barca parte da ferma in t₀ e aumenta la sua velocità fino al momento t₁ in cui raggiunge 4,12m/s con accelerazione costante.

d1) qual è la velocità media della barca nel tragitto percorso tra t₀ e t₁?

d2) se alla barca occorrono 4,77s per raggiungere la suddetta velocità, che distanza ha percorso in tale intervallo di tempo?

d1) La velocità media in valore assoluto è

v_m = (v_f + v_i) / 2

v_m = (4,12m/s + 0_i) / 2 = 2,06m/s

d2) per calcolare la distanza useremo la legge oraria del moto uniformemente accelerato

s_f = s_i + v_i t + ½ a t²

ci manca l’accelerazione, che ricaveremo dalla legge della velocità uniformemente accelerata (sapendo quanto tempo ha impiegato l’accelerazione per aumentare la velocità da zero a 4,12m/s)

v_f = v_i + a t

4,12m/s = 0 + a*4,77s, dal che

a = 4,12m/s/4,77s = 0,863m/s², valore che inseriremo nella legge oraria

s_f = 0 + 0* t + ½*0,863m/s²*(4,77s )² = 9,826m

↑2010.10.15 Legge oraria in moti rettilinei uniformi: qui un esempio (Luigi inizia a camminare andando verso un bar che dista 108m … Matilde parte nello stesso tempo dal bar, ma si ferma un po’, poi riprende …)